THE LYDIAN MODE
4 Settembre 2020
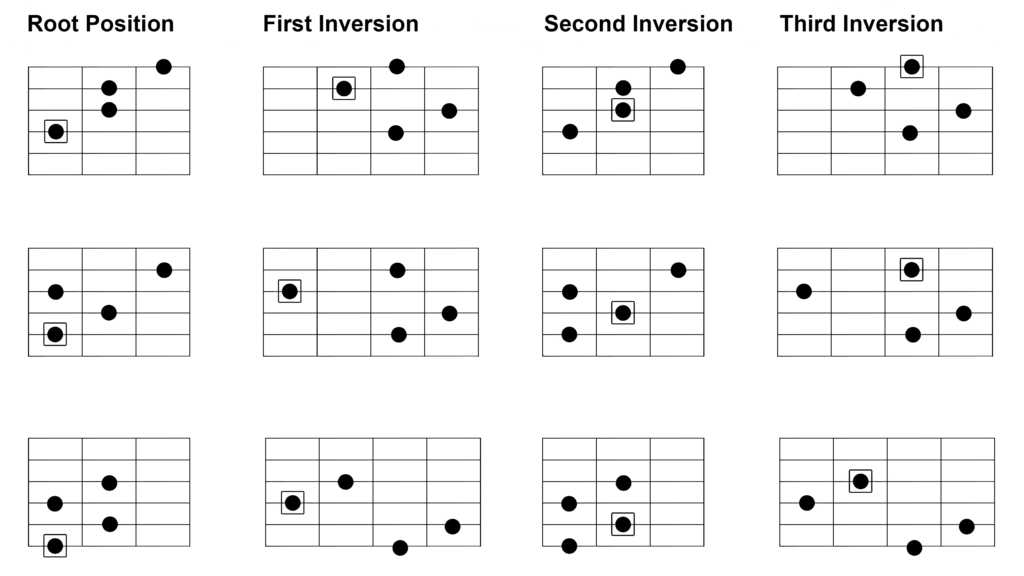
LE TRIADI. FORME BASE
14 Settembre 2020Dominant Chords with Altered 5th
If last time I was talking about Dominant chords with an altered 9th, now I’m going to deal with the alteration of the 5th.
7(b5)
The 7(b5) chord is basically a symmetrical chord. Olivier Messiaen would define it a chord with limited transposition: the 7(b5) is enharmonically equal to its tritone transposition. For instance:
C7(b5) = Gb7(b5)
C E Gb Bb Gb Bb Dbb Fb
We find this chord in the harmonization of both the diminished and whole-tone scales, but it can also be built on the IV degree of the melodic minor.
If we add two of these chords a 3rd apart we end up with a complete diminished scale. In the same way, two 7(b5) chords a tone apart give us the six notes of a whole-tone scale.
| C7(b5) | + | Eb7(b5) |
| C E Gb Bb | Eb G Bbb Db = C Db Eb E Gb G A Bb (C dim S-T) | |
| + | D7(b5) = C D E Gb Ab Bb | |
| D F# Ab C |
On the guitar we can play the 7(b5) chord like this:
7(#5)
The harmonization of the whole-tone scale and the melodic minor also gives us the 7(#5) chord, while there is no such chord in the diminished scale.
On the melodic minor scale we find it on the V and VII degrees.
Even if it’s not a symmetrical chord as the 7(b5), the augmented triad on which it is built is.
In a D melodic minor scale we find A7(#5) and C#7(#5), a major 3rd apart and both containing the augmented triad F – A – C#. They only differ for the minor 7th: G in the first and B in the second chord.

Sound Experiments
Let’s now make an experiment with the 7(#5) chord.
Imagine being in D melodic minor: D-E-F-G-A-B-C#. If we consider the augmented triad, each one of its notes could be considered as the fundamental tone. Just like we talked about A7(#5) and C#7(#5), both containing the triad A-C#-F, we can consider F as fundamental and build an F7(#5).
This chord (F-A-C#-Eb) introduces the note Eb, shifting the sound towards the whole-tone scale:
| F – A – C# | + | Eb | F7(#5) |
| G | A7(#5) | ||
| B | C#7(#5) |



